AMM最终条记：五大类无常损失解决方案

媒介 ——《AMM最终条记》是对诸多代表性 AMM 项目和相关论文举行的一项综述（survey），因为 AMM 所涉及层面较为遍及，本文选取我们认为最能代表 AMM 本质特征以及将来成长偏向的无常损失举行解说。

注：AMM（Automated Market Maker），自动化做市商，以根基数学曲线界说加密钱币生意业务对的供需曲线，基于智能合约的全天候无人值守，从头界说了 DEX 的根基形态，代表项目 Uniswap。

各人最为体贴的无常损失是一个难题，不行解，但存在优化的要领。

从简朴的角度来说，无常损失就是就地外（AMM 资金池外的主流生意业务市场）代币 A 相对于代币 B 的汇率上涨时，套利生意业务者会从场外筹集代币 B，并转移到 AMM 资金池，以相对于场外更优惠的汇率换得更多的代币 A，从而实现无风险套利。而这部门利润也是资金池（LP）的损失，可以称之为无常损失（姑且损失），由于一旦汇率又从头归到原始位置，将再次缔造反向套利空间（对称的），整体池子的资产数目将归回到原始状态，LP 们无损失，但由于行情的两次变化，也因此造福了两次套利者利润，这个利润空间就不再来自于 LP 的财富，而是市场时机，是只有精明的套利者不停盯市场赢得的时机。从这个角度望，无常损失是精明的套利者和怀揣大局意识的 LP 之间博弈平衡的成果，套利者也极大地活跃了 AMM 生意业务市场，尤其是当有很是多的套利者开始意识到此处的时机并开始竞争套利。

从一般性的角度界说无常损失，即无常损失只望生意业务对汇率是否产生变化，一旦产生变更，便发生客观的无常损失，与是涨是跌无关，一旦汇率归回，损失自动消失。这意味着，只有当流动性提供者（LP）在与最初使用的代价环境差别的环境下移除流动性时，才会呈现无常损失。假如不移除，而等候一个更有时机的机会撤出，损失就不会产生。作为对比，在传统金融上，我们可以认为这是一个?"卖出永续跨期?"的头寸。之所以说是永续，是由于这个头寸没有到期日，LP 可以持有多久就持有多久。

另外要着重提到的一点，也是如今许多玩家都未意识到的一个方面，无常损失虽然理论上是无上限的，但基于比特币等大行情的变更老是有所规模的假设，无常损失也是有可计较的上限，比方生意业务对 BTC/USDT 中 BTC 从 20000 USDT 涨到 60000 USDT，留给套利者的无常损失空间也不会凌驾 13%，即 LP 无常损失节制在 13%（无常损失计较器：https://yieldfarmingtools.com/tools）。

别的，无常损失是一种贪婪心理，我们老是爱将现实和如果做对比，照旧望 BTC/USDT 生意业务对，在 BTC 上涨后，本质上岂论怎么无常损失，LP 的财富老是法币增值的，然而人们去去爱跟如果做对比，会想“如果本身当初在 20000 USDT 的时候一直持有这么多 BTC 而不往介入 AMM 卖掉该多好”，但实际上许多 LP 是由于 AMM 才开始组建本身的资产设置，往购置 BTC，往构建生意业务对，因此大大都 LP 财富增值的时机恰是来自于 AMM 这种集储备利钱与基金组合功效于一身的特定场景，假如老是抱着贪婪的心态往对待问题，那么可以必定任何金融市场均不存在只有收益没有风险的路径。

附：以下为模拟生意业务：（1）当 1 ETH = 500 USDT，做市商存进 10 ETH 和 5000 USDT。他的总资产价值是10000 USDT。（2）当 1 ETH = 550 USDT，这个时候就存在套利的空间，在 AMM 机制下，做市商池就会自动向套利者卖出 ETH 调换 USDT，因此，今朝流动性池中资产变为 9.53 个 ETH 和 5244 个 USDT，对应的 ETH 的代价为 550 USDT，总资产价值是 10488 USDT。（3）假如不往做市，USDT 本位的价值为 10500，这便发生了相对的 12 USDT 无常损失。?相反的，（a）当代价下跌 1 ETH = 450 USDT 时，套利者会向池子注进 ETH 来调换有利润空间的 USDT，直到 ETH 的场内代价与市场价沟通，因此做市商的流动池就变为 10.54 ETH 和 4743 USDT，总资产价值是 9486 USDT。（b）假如不举行做市勾当，总资产价值是 9500 USDT。相对来望整体资产贬值了 500 USDT，举行做市分外还损失 14 USDT。?从实际例子中不丢脸出岂论代价涨跌，在AMM机制下，流动性供给商的反向操作城市造成必然的无常损失。

动态权重的恒定加权几何平均函数

此类解决方案以 Bancor V2 为代表项目。最原始的灵感是 Balancer 为 AMM 引进了恒定几何加权平均的函数：

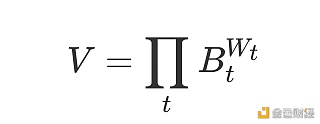
本质跟 Uniswap 的恒定乘积雷同，但赋予了每一项指数（权重）的观点，也因此拥有更机动的曲线形态。也是 Balancer 第一次在一篇文章（Interest-Bearing Stablecoin Pools Without Impermanent Loss https://medium.com/balancer-protocol/zero-impermanent-loss-stablecoin-pool-with-lending-interests-a3da6d8bb782）中提到了可以通过动态更新权重项来从泉源上阻止无常损失的产生，而 Bancor V2 则对此方案举行了更通用细致的数学描述（Calculating Dynamic Reserve Weights in Bancor V2 https://blog.bancor.network/calculating-dynamic-reserve-weights-in-bancorv2-538b901bcac4）（pdf 版本 https://drive.google.com/file/d/1lYsaUi5du7BdP5eXgVJX60POcg2UkBfZ/view）。

细致的数学描述这里不铺开解说，因为篇幅限制本文只举行道理提要。假如权重项稳定的话，可以将曲线形态当作跟 Uniswap 一样。假如不停变化权重，曲线将会绕着曲线上的某一个点在不停旋转，使得旋转后的曲线在该点的切线斜率（即汇率）与最新的市场代价保持一致，而促入这个旋转计较的便是来自外部市场价的预言机驱动，通过为 AMM 更新每一刻最新的市场价，反推权重项的计较，以使当前点（池子两资产数目构成的点）在新曲线的切线斜率不停随市场变化，入而不缔造套利空间。形象的计较如下：

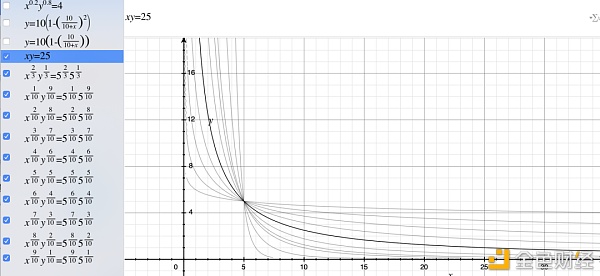
虽然此类解决问题的要领长短常本质的，但缺陷也是十分明明且隐患巨大。一个原来可以完全自动应对市场的 AMM 需要单点依靠一个外部预言机，一旦预言机呈现问题，即便是很小的问题，也会给 AMM 带来巨大的套利攻击损失，这种损失差别于无常损失，是切切实实的用户损失，也会给以后 AMM 的贸易扩大带来底子阻力。另外，此类 AMM 将彻底失往市场订价权，即抛却了本身成为 Primary Market，我们都知道跟着 DeFi 等的崛起，越来越多有价值的新资产都选择 DEX 作为本身的 Primary Market，反而那些中央化的主流生意业务所成了 Secondary Market。

除了 Bancor V2，国产项目 DODO 也有着雷同的方式，虽然 DODO 并未接纳恒定加权几何平均函数，而是接纳了一种雷同 Curve 的混淆机关函数，但本质都是依靠一个外部预言机，来不停更改【订价/生意业务】曲线的形态，使得新曲线的报价成果与外部市场精密追随。

假如一个系统只依靠本身，那么它的宁静界限就是本身，是可以计较的；假如一个系统依靠了外部因子，它的宁静界限理论上是不行估算的，犹如一个拜占庭漫衍式系同一样，没有任何经验调查甚至形式化数学可以估算笼罩到所有潜在 fault（妨碍）路径。

虚拟余额限制套路路径

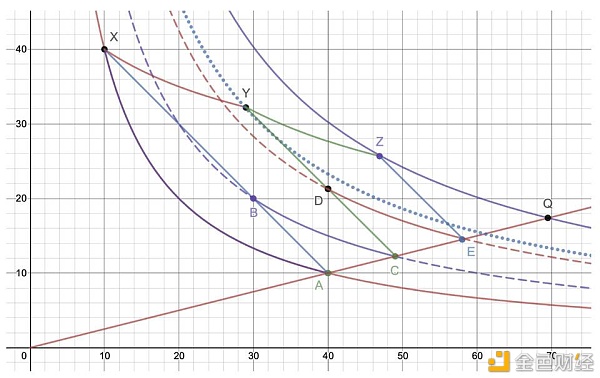
此类仅存在于 Mooniswap。与 Bancor V2 和 DODO 解决问题的思维差别，Mooniswap 并未改变 AMM 的最大本质（自动自主订价），与 Uniswap 只能眼睁睁望着套利者来吃肉差别，当系统呈现套利空间时，Mooniswap 会自动按照偏移量逐次构建多条虚拟的曲线，使得套利生意业务者只能接收到每一条虚拟曲线所划定的套利上限，而不再是一次性在原始曲线上完成大量套利。

如下图，初始均衡点在 A，一笔生意业务使得系统处于 X 点，此时便发生了套利空间，在 Uniswap 这种传统 AMM 中，任何智慧的套利者都可以通过一笔生意业务一次性地拉归到 A 点，而这个历程去去陪同着可观的利润。Mooniswap 的虚拟机关法便是陆续构建了上面三条 AMM 曲线，首先给套利者出现的是下图第二条曲线 BC，套利者的套利路径仅仅只有 B 到 C 的短暂历程，当该套利者达到 C 点后，系统便放出第二条虚拟曲线 DE，同理，给套利者出现 D 到 E 的套利路径，在第二个套利者达到 E 点后，系统放出最后一条曲线，也是终极要更迭到的实际曲线 ZQ，最后一位套利者从 Z 到 Q 完成套利，终极系统曲线变为 ZQ，且均衡点为 Q。通过者一系列虚拟机关，即便三次加起来的套利空间也遥小于传统 AMM 曲线一次套利路径，并且在这个历程中套利者也为资金池注进了更多的资产，使得池子范围变大，也充当了 LP，曲线向右上偏移。

对于详细的点位计较和数学证实，请详见 Mooniswap 白皮书（Mooniswap https://mooniswap.exchange/docs/MooniswapWhitePaper-v1.0.pdf）。

此类要领缺点，需要仔细鉴别套利时机的呈现，必然水平上也需要依靠外部因子；并且虚拟量缩短套利路径的历程需要动态构建大量曲线，对于高并发的系统，此类要领在工程上过于庞大，引进太多不确定性。

无穷网格计谋做市

以比原链 MOV 超导 V2 提出的基于无穷网格计谋的 AMM 算法为例（暂未实现）。这种解决方案并未直接往存眷无常损失的产生（如前第一类），也未往针对无常损失的始作俑者套利者（第二类），它是在以一种基金司理的脚色在办理 LP 的财富，不但愿只通过储备利钱（手续费）让 LP 财富增值，更是但愿可以在专业基金计谋的感化下充实操纵好 LP 巨大的财富池，追随市场局势，得到基金式的财富增值。个中，无穷网格计谋是 MOV 超导 V2 所选择的偏向，并将其在 AMM 上实现，虽然另有许多不足，但如下大抵给出了构建思路。

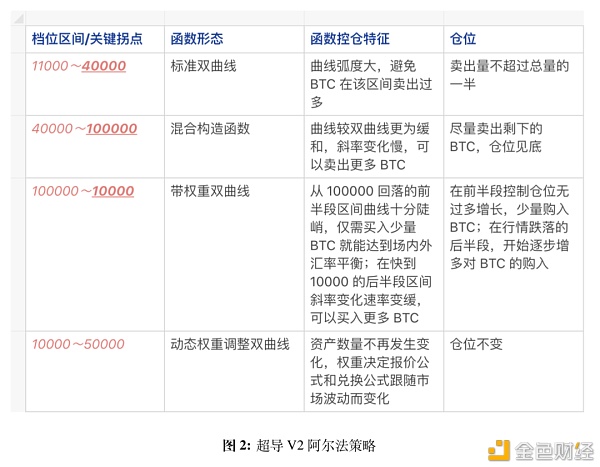
如上图，超导 V2 在原有恒定乘积曲线做市商机制的基础长进一步分段机关出了差别形态的曲线形态，以满意无穷网格的根基界说——“分段买进卖出，即便在市场最高点时也有现货可以卖出，在市场最低点时也能完成建仓操作”。超导 V2 通过上面四种分段函数的机关，但愿可以实现——“在行情上涨时，可以或许适当出货 BTC，但不要大量出货，慢慢逐量，既可以或许帮 LP 在到达最高点前守住 BTC，也可以或许在上涨行情中智能化的卖出适当数目 BTC，以应对潜在的大跌风险；在行情下跌时，HOLD，以上涨时积聚的 USDT 财富得到财富增值”。

在详细函数机关和实现道理上，可以对照上图望如下图例。早在 2020 年 8 月份（BTC 11000 刀，超导 V2 理论方才降生时），其时的超导 V2 设计者就估计将来可能会到达一个 40000 刀至 100000 刀的一个牛市行情，因此做了如上四个分段预测。在第一段中，超导函数为很是普通的恒定乘积曲线，执行简朴的 AMM 仓位计谋，在到达 40000 刀时，函数自动触发切换为混淆机关函数曲线，这是一种曲率更低的曲线，可以大幅度改变 BTC 仓位，在 40000 ～ 100000 规模，假如判断本轮最高点可能到 100000 刀，则在 100000 刀处再次配置函数切换点，变为很是陡峭的双曲线，可以帮忙 LP 在行情归落历程中不会从头将高点套现的 USDT 再还归去。详细数据可以见下图。

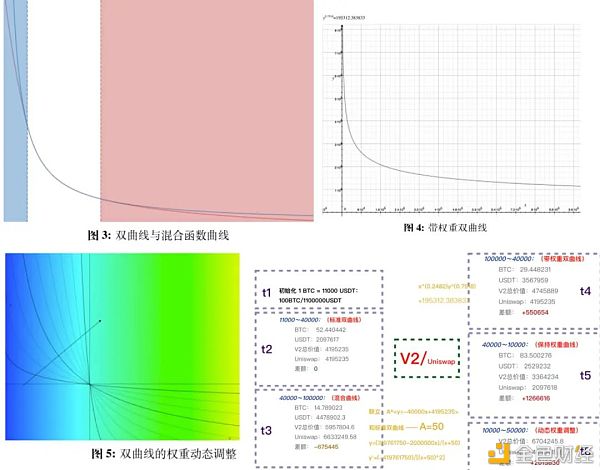
这种解决方案的上风是一旦计谋预测乐成，不仅可以解决无常损失，还可以大幅度帮忙 LP 得到基金级此外财富增值，这是市道市情上任何 AMM 都给不了的，即便是有流动性挖矿加持。并且这种计谋不依靠任何外部因子，只依靠自身计谋，因此不会引进其他风险，即便是后市行情不如所愿，也可以提前更改下一个函数切换点，实时改变下一段函数形态，制止大范围损失。缺陷也是十分明明的，即需要很是专业的基金司理预判和计谋，需要可以或许预测好较大规模的后市行情，并且分段函数的机关十分庞大，超导 V2 在构建自身计谋时，实在是有更好的函数机关，但迫于数学形态过于庞大且工程实现坚苦，便选择了如上实现案例，也是一种折衷措施。

经济赔偿

这一类是最为各人认识的要领，即以自身代币的形式为 LP 赔偿损失，包括 Bancor V2.1 和流动性挖矿两种形式。

Bancor V2.1 是在 Bancor 意识到 Bancor V2（如上第一类）无法解决无常损失并且会带来预言机系统风险之后从头拟定的无常损失方案，这种要领会从系统层面记载每一个 LP 初始做市时的仓位，在无常损失产生后，会通过系统增发 Bancor 代币来赔偿无常损失。

流动性挖矿也是异曲同工，不外 Bancor V2.1 的赔偿更为精细，有几多损失便补助几多自身代币。而市道市情上的流动性挖矿，多则 APY 可达几十倍，少则也有两三倍，是一场疯狂的造富运动，即便是 LP 介入了一个月，所得到的挖矿财富也足够其应对无常损失的任何上限。

因此流动性挖矿假如可以做好“善后”事情，也未尝不是一种底子性的无常损失解决方案。

期权对冲

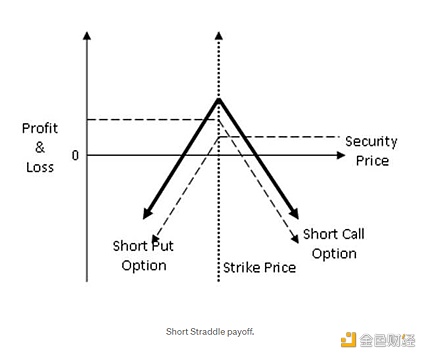
也鸣 Hedge，这一类研究很是稀少，险些不见于任何市道市情上的项目，之前火币研究院有过一篇专门的陈诉（AMM做市无常损失对冲阐明系列一：损益及期权对冲模子构建 https://zhuanlan.zhihu.com/p/260141168）。火币研究院的文章论证了通过望跌期权来赔偿无常损失的根基结论，并给出了详细数目和位置指导，必然水平上是可以明明起到缓解无常损失的感化，见下图。

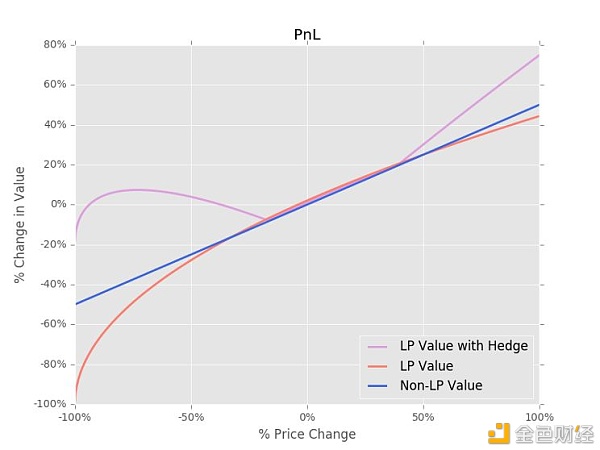
厥后我们也掘客了几篇很是好的行业论文，尤其是 Placeholder 的研究员 Alex Evans 的研究事情（论文 When does the tail wag the dog? Curvature and market making 和论文 Liquidity Provider Returns in Geometric Mean Markets）十分凸起，我们也在此对其举行简朴解读。

在传统金融理论中，动态套期保值是机构投资者操纵股指期货或股票与无风险资产缔造合成的望跌期权并通过使用合成望跌期权计谋寻求掩护投资组合价值的计谋。而在 CFMM 机制下，有人提出可以类比资产的 Delta 值（δ）和 Gamma（γ）值来规避高额 LP 风险。接下来我们将管帐算 LP 的动态对冲数目，并铺示它们如安在生意业务中体现杰出。通过以下的数学推导，我们还可以望出动态对冲数目和曲率之间的关系。

储蓄的投资组合价值

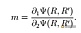
。则等式满意函数 ψ 对市场价 m 求一阶导为零，带进得：

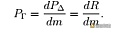
在 Joseph Clark 所著的论文《The replicating portfolio of a constant product market》中，他提出了用带 CPM 收益的欧式期权来进步 LP 的收益。在他望来，LP 按照新的资产比例获得的必然比例的生意业务用度可以被准确复制与期货和期权的静态组合。假如这些期货和期权存在而且是可生意业务的，每千次铺示用度收取的生意业务用度将由期权代价决定和预期的生意业务量。假如期货和期权不存在，则 CPM 的收益可以用来创建它们。

我们可以具体接头下在 CPM 模式下的收益以及终极组合投资的总收益。

我们假定当前市场价为

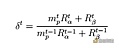
复制期权的总归报即是CPM收益和期货的原有收益相加：

综上我们不丢脸出，Joseph Clark 认为可以用静态资产组合来对冲 LP 的风险损失，而动态对冲数目和曲率有紧密亲密接洽。若期权和期货不行生意业务，那么 CPM 带来的收益也可以作为复制期权的备选项。

未完待续

我们另有许多课题和最新研究结果与各人分享，包括

（1）LP 最终收益的数学公式表达以及影响 LP 收益的最本质因子，实在都可以通过公式论证出来，以帮忙 AMM 产物更好的举行迭代改良，比方影响 LP 收益的有曲率、informed trading 等；

（2）流动性挖矿（Yield Farming）的真正使命，除了赔偿无常损失外，还可以起到很是好的 AMM 项目自身原始代币的刊行以及代币代价不变的感化，我们认为通过流动性挖矿刊行的自身代币代价，不会存在灭亡螺旋的现象，反而会培养项目市值的一个强支撑，固然条件是该项目长短常有人气有口碑的项目，别的，流动性挖矿的详细补助数值也存在数学表达和影响因子；

（3）AMM 项目在将来会都向着动态 AMM 形态成长，即不再局限于一条曲线形态，会按照差别的情境辅助以多种曲线形态；曲率是一个被大大忽略的曲线研究范畴，曲率险些决定着一切 AMM 产物特征，曲率甚至可以改变一个新币种的主市场订价问题

作者：王嘉昊 刘秋杉

来历：比原链研究院